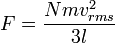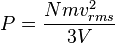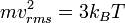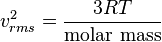Tampilkan postingan dengan label Fisika SMA XI. Tampilkan semua postingan
Tampilkan postingan dengan label Fisika SMA XI. Tampilkan semua postingan
Selasa, 10 April 2012
1. Gerak Lurus Beraturan (GLB)
KINEMATIKA adalah Ilmu gerak yang membicarakan gerak suatu benda tanpa memandang gaya yang bekerja pada benda tersebut (massa benda diabaikan). Jadi jarak yang ditempuh benda selama geraknya hanya ditentukan oleh kecepatan v dan atau percepatan a.
Gerak Lurus Beraturan (GLB) adalah gerak lurus pada arah mendatar dengan kocepatan v tetap (percepatan a = 0), sehingga jarakyang ditempuh S hanya ditentukan oleh kecepatan yang tetap dalam waktu tertentu.
Pada umumaya GLB didasari oleh Hukum Newton I ( S F = 0 ).
Tanda D (selisih) menyatakan nilai rata-rata.
Tanda d (diferensial) menyatakan nilai sesaat.
2. Gerak Lurus Berubah Beraturan (GLBB)
Gerak Lurus Berubah Beraturan (GLBB) adalah gerak lurus pada arah mendatar dengan kecepatan v yang berubah setiap saat karena adanya percepatan yang tetap. Dengan kata lain benda yang melakukan gerak dari
keadaan diam atau mulai dengan kecepatan awal akan berubah kecepatannya karena ada percepatan (a= +) atau perlambatan (a= -).
Pada umumnya GLBB didasari oleh Hukum Newton II ( S F = m . a ).
vt = kecepatan sesaat benda
v0 = kecepatan awal benda
S = jarak yang ditempuh benda
f(t) = fungsi dari waktu t
Syarat : Jika dua benda bergerak dan saling bertemu maka jarak yang ditempuh kedua benda adalah sama.
3. Grafik Gerak Benda
Grafik gerak benda (GLB dan GLBB) pada umumnya terbagi dua, yaitu S-t dan grafik v-t.
Pemahaman grafik ini penting untuk memudahkan penyelesaian soal.
Khusus untuk grafik v-t maka jarak yang ditempuh benda dapat dihitung dengan cara menghitung luas dibawah kurva grafik tersebut.
4. Gerak Karena pengaruh Gravitasi
g = percepatan gravitasi bumi.
y = h = lintasan yang ditempuh benda pada arah vertikal,(diukur dari posisi benda mula-mula).
t = waktu yang dibutuhkan benda untuk menempuh lintasannya.
syarat suatu benda mencapai tinggi maksimum (h maks): Vt = 0
Dalam penyelesaian soal gerak vertikal keatas, lebih mudah diselesaikan dengan menganggap posisi di tanah adalah untuk Y = 0.
Contoh:
1. Sebuah partikel bergerak sepanjang sumbu-X dengan persamaan lintasannya: X = 5t2 + 1, dengan X dalam meter dan t dalam detik. Tentukan:
a. Kecepatan rata-rata antara t = 2 detik dan t = 3 detik.
b. Kecepatan pada saat t = 2 detik.
c. Jarak yang ditempah dalam 10 detik.
d. Percepatan rata-rata antara t = 2 detik dan t = 3 detik.
Jawab:
a. v rata-rata = DX / Dt = (X3 - X2) / (t3 - t2) = [(5 . 9 + 1) - (5 . 4 + 1)] / [3 - 2] = 46 - 21 = 25 m/ detik
b. v2 = dx/dt |t=2 = 10 |t=2 = 20 m/detik.
c. X10 = ( 5 . 100 + 1 ) = 501 m ; X0 = 1 m
Jarak yang ditempuh dalam 10 detik = X10 - X0 = 501 - 1 = 500 m
d. a rata-rata = Dv / Dt = (v3- v2)/(t3 - t2) = (10 . 3 - 10 . 2)/(3 - 2) = 10 m/det2
2. Jarak PQ = 144 m. Benda B bergerak dari titik Q ke P dengan percepatan 2 m/s2 dan kecepatan awal 10 m/s. Benda A bergerak 2 detik kemudian dari titik P ke Q dengan percepatan 6 m/s2 tanpa kecepatan awal. Benda A dan B akan bertemu pada jarak berapa ?
Jawab:
Karena benda A bergerak 2 detik kemudian setelah benda B maka tB = tA + 2.
 SA = v0.tA + 1/2 a.tA2 = 0 + 3 tA2
SA = v0.tA + 1/2 a.tA2 = 0 + 3 tA2
SB = v0.tB + 1/2 a.tB2 = 10 (tA + 2) + (tA + 2)2
Misalkan kedua benda bertemu di titik R maka
SA + SB = PQ = 144 m
3tA2 + 10 (tA + 2) + (tA + 2)2 = 144
2tA2 + 7tA - 60 = 0
Jadi kedua benda akan bertemu pada jarak SA = 3tA2 = 48 m (dari titik P).
3. Grafik di bawah menghubungkan kocepatan V dan waktu t dari dua mobil A dan B, pada lintasan dan arah sama. Jika tg a = 0.5 m/det, hitunglah:
a. Waktu yang dibutuhkan pada saat kecepatan kedua mobil sama.
b. Jarak yang ditempuh pada waktu menyusul
Jawab:
 Dari grafik terlihat jenis gerak benda A dan B adalah GLBB dengan V0(A) = 30 m/det dan V0(B) = 0.
Dari grafik terlihat jenis gerak benda A dan B adalah GLBB dengan V0(A) = 30 m/det dan V0(B) = 0.
a. Percepatan kedua benda dapat dihitung dari gradien garisnya,
jadi : aA = tg a = 0.5
10/t = 0.5 ® t = 20 det
aB = tg b = 40/20 = 2 m/det
b. Jarak yang ditempuh benda
SA = V0 t + 1/2 at2 = 30t + 1/4t2
SB = V0 t + 1/2 at2 = 0 + t2
pada saat menyusul/bertemu : SA = SB ® 30t + 1/4 t2 = t2 ® t = 40 det
Jadi jarak yang ditempuh pada saat menyusul : SA = SB = 1/2 . 2 . 402 = 1600 meter
5. Gerak Berbentuk Parabola
Gerak ini terdiri dari dua jenis, yaitu:
1. Gerak Setengah Parabola
Benda yang dilempar mendatar dari suatu ketinggian tertentu dianggap tersusun atas dua macam gerak, yaitu :
2. Gerak Parabola/Peluru
Benda yang dilempar ke atas dengan sudut tertentu, juga tersusun atas dua macam gerak dimana lintasan
dan kecepatan benda harus diuraikan pada arah X dan Y.
Syarat mencapai titik P (titik tertinggi): vy = 0
top = v0 sin q / g
sehingga
top = tpqtoq = 2 top
OQ = v0x tQ = V02 sin 2q / g
h max = v oy tp - 1/2 gtp2 = V02 sin2 q / 2g
vt = Ö (vx)2 + (vy)2
Contoh:
1. Sebuah benda dijatuhkan dari pesawat terbang yang sedang melaju horisontal 720 km/jam dari ketinggian 490 meter. Hitunglah jarak jatuhnya benda pada arah horisontal ! (g = 9.8 m/det2). Jawab:
2. Peluru A dan peluru B ditembakkan dari senapan yang sama dengan sudut elevasi yang berbeda; peluru A dengan 30o dan peluru B dengan sudut 60o. Berapakah perbandingan tinggi maksimum yang dicapai peluru A dan peluru B?
Jawab:
Peluru A:
hA = V02 sin2 30o / 2g = V02 1/4 /2g = V02 / 8g
Peluru B:
hB = V02 sin2 60o / 2g = V02 3/4 /2g = 3 V02 / 8g
hA = hB = V02/8g : 3 V02 / 8g = 1 : 3
6. Gerak Melingkar
Gerak melingkar terbagi dua, yaitu:
1. GERAK MELINGKAR BERATURAN (GMB)
GMB adalah gerak melingkar dengan kecepatan sudut (w) tetap.
2. GERAK MELINGKAR BERUBAH BERATURAN (GMBB)
GMBB adalah gerak melingkar dengan percepatan sudut a tetap.
Dalam gerak ini terdapat percepatan tangensial aT = percepatan linier, merupakan percepatan yang arahnya menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan v).
a = Dw/Dt = aT / R
aT = dv/dt = a R
T = perioda (detik)
R = jarijari lingkaran.
a = percepatan angular/sudut (rad/det2)
aT = percepatan tangensial (m/det2)
w = kecepatan angular/sudut (rad/det)
q = besar sudut (radian)
S = panjang busur
Hubungan besaran linier dengan besaran angular:
Contoh:
1. Sebuah mobil bergerak pada jalan yang melengkung dengan jari-jari 50 m. Persamaan gerak mobil untuk S dalam meter dan t dalam detik ialah:
S = 10+ 10t - 1/2 t2
Hitunglah:
Kecepatan mobil, percepatan sentripetal dan percepatan tangensial pada saat t = 5 detik !Jawab:
v = dS/dt = 10 - t; pada t = 5 detik, v5 = (10 - 5) = 5 m/det.
- percepatan sentripetal : aR = v52/R = 52/50 = 25/50 = 1/2 m/det2
- percepatan tangensial : aT = dv/dt = -1 m/det
KINEMATIKA adalah Ilmu gerak yang membicarakan gerak suatu benda tanpa memandang gaya yang bekerja pada benda tersebut (massa benda diabaikan). Jadi jarak yang ditempuh benda selama geraknya hanya ditentukan oleh kecepatan v dan atau percepatan a.
Gerak Lurus Beraturan (GLB) adalah gerak lurus pada arah mendatar dengan kocepatan v tetap (percepatan a = 0), sehingga jarakyang ditempuh S hanya ditentukan oleh kecepatan yang tetap dalam waktu tertentu.
Pada umumaya GLB didasari oleh Hukum Newton I ( S F = 0 ).
S = X = v . t ; a = Dv/Dt = dv/dt = 0
|
v = DS/Dt = ds/dt = tetap
|
Tanda D (selisih) menyatakan nilai rata-rata.
Tanda d (diferensial) menyatakan nilai sesaat.
2. Gerak Lurus Berubah Beraturan (GLBB)
Gerak Lurus Berubah Beraturan (GLBB) adalah gerak lurus pada arah mendatar dengan kecepatan v yang berubah setiap saat karena adanya percepatan yang tetap. Dengan kata lain benda yang melakukan gerak dari
keadaan diam atau mulai dengan kecepatan awal akan berubah kecepatannya karena ada percepatan (a= +) atau perlambatan (a= -).
Pada umumnya GLBB didasari oleh Hukum Newton II ( S F = m . a ).
vt = v0 + a.t
vt2 = v02 + 2 a S
S = v0 t + 1/2 a t2
|
v0 = kecepatan awal benda
S = jarak yang ditempuh benda
f(t) = fungsi dari waktu t
v = ds/dt = f (t)
a = dv/dt = tetap
|
3. Grafik Gerak Benda
Grafik gerak benda (GLB dan GLBB) pada umumnya terbagi dua, yaitu S-t dan grafik v-t.
Pemahaman grafik ini penting untuk memudahkan penyelesaian soal.
Khusus untuk grafik v-t maka jarak yang ditempuh benda dapat dihitung dengan cara menghitung luas dibawah kurva grafik tersebut.
| GRAFIK GLB (v = tetap ; S - t)  | GRAFIK GLBB (a = tetap ; v - t ; S - t2) |
| GERAK JATUH BEBAS: | adalah gerak jatuh benda pada arah vertikal dari ketinggian h tertentu tanpa kecepatan awal (v0 = 0), jadi gerak benda hanya dipengaruhi oleh gravitasi bumi g. |
y = h = 1/2 gt2t = Ö(2 h/g)
yt = g t = Ö(2 g h) |
y = h = lintasan yang ditempuh benda pada arah vertikal,(diukur dari posisi benda mula-mula).
t = waktu yang dibutuhkan benda untuk menempuh lintasannya.
| GERAK VERTIKAL KE ATAS: | adalah gerak benda yang dilempar dengan suatu kecepatan awal v0 pada arah vertikal, sehingga a = -g (melawan arah gravitasi). |
Dalam penyelesaian soal gerak vertikal keatas, lebih mudah diselesaikan dengan menganggap posisi di tanah adalah untuk Y = 0.
Contoh:
1. Sebuah partikel bergerak sepanjang sumbu-X dengan persamaan lintasannya: X = 5t2 + 1, dengan X dalam meter dan t dalam detik. Tentukan:
a. Kecepatan rata-rata antara t = 2 detik dan t = 3 detik.
b. Kecepatan pada saat t = 2 detik.
c. Jarak yang ditempah dalam 10 detik.
d. Percepatan rata-rata antara t = 2 detik dan t = 3 detik.
Jawab:
a. v rata-rata = DX / Dt = (X3 - X2) / (t3 - t2) = [(5 . 9 + 1) - (5 . 4 + 1)] / [3 - 2] = 46 - 21 = 25 m/ detik
b. v2 = dx/dt |t=2 = 10 |t=2 = 20 m/detik.
c. X10 = ( 5 . 100 + 1 ) = 501 m ; X0 = 1 m
Jarak yang ditempuh dalam 10 detik = X10 - X0 = 501 - 1 = 500 m
d. a rata-rata = Dv / Dt = (v3- v2)/(t3 - t2) = (10 . 3 - 10 . 2)/(3 - 2) = 10 m/det2
2. Jarak PQ = 144 m. Benda B bergerak dari titik Q ke P dengan percepatan 2 m/s2 dan kecepatan awal 10 m/s. Benda A bergerak 2 detik kemudian dari titik P ke Q dengan percepatan 6 m/s2 tanpa kecepatan awal. Benda A dan B akan bertemu pada jarak berapa ?
Jawab:
Karena benda A bergerak 2 detik kemudian setelah benda B maka tB = tA + 2.

SB = v0.tB + 1/2 a.tB2 = 10 (tA + 2) + (tA + 2)2
Misalkan kedua benda bertemu di titik R maka
SA + SB = PQ = 144 m
3tA2 + 10 (tA + 2) + (tA + 2)2 = 144
2tA2 + 7tA - 60 = 0
Jadi kedua benda akan bertemu pada jarak SA = 3tA2 = 48 m (dari titik P).
3. Grafik di bawah menghubungkan kocepatan V dan waktu t dari dua mobil A dan B, pada lintasan dan arah sama. Jika tg a = 0.5 m/det, hitunglah:
a. Waktu yang dibutuhkan pada saat kecepatan kedua mobil sama.
b. Jarak yang ditempuh pada waktu menyusul
Jawab:

a. Percepatan kedua benda dapat dihitung dari gradien garisnya,
jadi : aA = tg a = 0.5
10/t = 0.5 ® t = 20 det
aB = tg b = 40/20 = 2 m/det
b. Jarak yang ditempuh benda
SA = V0 t + 1/2 at2 = 30t + 1/4t2
SB = V0 t + 1/2 at2 = 0 + t2
pada saat menyusul/bertemu : SA = SB ® 30t + 1/4 t2 = t2 ® t = 40 det
Jadi jarak yang ditempuh pada saat menyusul : SA = SB = 1/2 . 2 . 402 = 1600 meter
5. Gerak Berbentuk Parabola
Gerak ini terdiri dari dua jenis, yaitu:
1. Gerak Setengah Parabola
Benda yang dilempar mendatar dari suatu ketinggian tertentu dianggap tersusun atas dua macam gerak, yaitu :
| a. | Gerak pada arah sumbu X (GLB) vx = v0 Sx = X = vx t |  |
| b. | Gerak pada arah sumbu Y (GJB/GLBB) vy = 0 ]® Jatuh bebas y = 1/2 g t2 |
Benda yang dilempar ke atas dengan sudut tertentu, juga tersusun atas dua macam gerak dimana lintasan
dan kecepatan benda harus diuraikan pada arah X dan Y.
| a. | Arah sb-X (GLB) v0x = v0 cos q (tetap) X = v0x t = v0 cos q.t |  Gbr. Gerak Parabola/Peluru |
| b. | Arah sb-Y (GLBB)v0y = v0 sin q Y = voy t - 1/2 g t2 = v0 sin q . t - 1/2 g t2 vy = v0 sin q - g t |
top = v0 sin q / g
sehingga
top = tpqtoq = 2 top
OQ = v0x tQ = V02 sin 2q / g
h max = v oy tp - 1/2 gtp2 = V02 sin2 q / 2g
vt = Ö (vx)2 + (vy)2
Contoh:
1. Sebuah benda dijatuhkan dari pesawat terbang yang sedang melaju horisontal 720 km/jam dari ketinggian 490 meter. Hitunglah jarak jatuhnya benda pada arah horisontal ! (g = 9.8 m/det2). Jawab:
| vx = 720 km/jam = 200 m/det. h = 1/2 gt2 ® 490 = 1/2 . 9.8 . t2 t = 100 = 10 detik X = vx . t = 200.10 = 2000 meter |  |
Jawab:
Peluru A:
hA = V02 sin2 30o / 2g = V02 1/4 /2g = V02 / 8g
Peluru B:
hB = V02 sin2 60o / 2g = V02 3/4 /2g = 3 V02 / 8g
hA = hB = V02/8g : 3 V02 / 8g = 1 : 3
6. Gerak Melingkar
Gerak melingkar terbagi dua, yaitu:
1. GERAK MELINGKAR BERATURAN (GMB)
GMB adalah gerak melingkar dengan kecepatan sudut (w) tetap.
 | Arah kecepatan linier v selalu menyinggung lintasan, jadi sama dengan arah kecepatan tangensial sedanghan besar kecepatan v selalu tetap (karena w tetap). Akibatnya ada percepatan radial ar yang besarnya tetap tetapi arahnya berubah-ubah. ar disebut juga percepatan sentripetal/sentrifugal yang selalu | v.
v = 2pR/T = w R
ar = v2/R = w2 R
s = q R
|
GMBB adalah gerak melingkar dengan percepatan sudut a tetap.
Dalam gerak ini terdapat percepatan tangensial aT = percepatan linier, merupakan percepatan yang arahnya menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan v).
a = Dw/Dt = aT / R
aT = dv/dt = a R
T = perioda (detik)
R = jarijari lingkaran.
a = percepatan angular/sudut (rad/det2)
aT = percepatan tangensial (m/det2)
w = kecepatan angular/sudut (rad/det)
q = besar sudut (radian)
S = panjang busur
Hubungan besaran linier dengan besaran angular:
| vt = v0 + a t wt S = v0 t + 1/2 a t2 | Þ w0 + a t Þ q = w0 + 1/2 a t2 |
1. Sebuah mobil bergerak pada jalan yang melengkung dengan jari-jari 50 m. Persamaan gerak mobil untuk S dalam meter dan t dalam detik ialah:
S = 10+ 10t - 1/2 t2
Hitunglah:
Kecepatan mobil, percepatan sentripetal dan percepatan tangensial pada saat t = 5 detik !Jawab:
v = dS/dt = 10 - t; pada t = 5 detik, v5 = (10 - 5) = 5 m/det.
- percepatan sentripetal : aR = v52/R = 52/50 = 25/50 = 1/2 m/det2
- percepatan tangensial : aT = dv/dt = -1 m/det
Teori Kinetik (atau teori kinetik pada gas) berupaya menjelaskan sifat-sifat makroscopik gas, seperti tekanan, suhu, atau volume, dengan memperhatikan komposisi molekular mereka dan gerakannya. Intinya, teori ini menytakan bahwa tekanan tidaklah
disebabkan oleh denyut-denyut statis di antara molekul-molekul, seperti yang diduga Isaac Newton, melainkan disebabkan oleh tumbukan antarmolekul yang bergerak pada kecepatan yang berbeda-beda. Teori Kinetik dikenal pula sebagai Teori Kinetik-Molekular atau Teori Tumbukan atau Teori Kinetik pada Gas.
Teori Kinetik juga telah diperluas untuk memasukkan tumbukan tidak lenting di dalam materi butiran oleh Jenkins dan kawan-kawan.[rujukan?]
Partikel memberi tumbukan kepada dinding sekali setiap 2l/vx satuan waktu (di mana l adalah panjang wadah). Kendati partikel menumbuk sebuah dinding sekali setiap 1l/vx satuan waktu, hanya perubahan momentum pada dinding yang dianggap, sehingga partikel menghasilkan perubahan momentum pada dinding tertentu sekali setiap 2l/vx satuan waktu.
Besaran kecepatan untuk tiap-tiap partikel mengikuti persamaan ini:
Misalkan ada sejumlah besar partikel yang bergerak cukup acak, gaay pada tiap-tiap dinding akan hampir sama dan kini perhatikanlah gaya pada satu dinding saja, kita punya:
 dapat dituliskan sebagai
dapat dituliskan sebagai 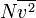 , di mana garis atas menunjukkan rata-rata, pada kasus ini rata-rata semua partikel. Kuantitas ini juga dinyatakan dengan
, di mana garis atas menunjukkan rata-rata, pada kasus ini rata-rata semua partikel. Kuantitas ini juga dinyatakan dengan  di mana vrms dalah akar kuadrat rata-rata kecepatan semua partikel.
di mana vrms dalah akar kuadrat rata-rata kecepatan semua partikel.
Jadi, gaya dapat dituliskan sebagai:
Jadi, karena luas bagian yang berseberangan dikali dengan panjang sama dengan volume, kita punya pernyataan berikut untuk tekanan
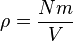 .
.
Maka tekanan adalah
 yakni suatu sifat mikroskopik. Ketahuilah bahwa hasil kali tekanan dan volume adalah sepertiga dari keseluruhan energi kinetik.
yakni suatu sifat mikroskopik. Ketahuilah bahwa hasil kali tekanan dan volume adalah sepertiga dari keseluruhan energi kinetik.
Derivat:

Suhunya menjadi
Dari persamaan 1 dan 3 didapat:
Karena 3N adalah derajat kebebasan (DK) dalam sebuah sistem gas monoatomik dengan N partikel, energi kinetik tiap DK adalah:
Assuming an ideal gas, a derivation[3] results in an equation for total number of collisions per unit time per area:
Other pioneers of the kinetic theory (which were neglected by their contemporaries) were Mikhail Lomonosov (1747),[4] Georges-Louis Le Sage (ca. 1780, published 1818),[5] John Herapath (1816)[6] and John James Waterston (1843),[7] which connected their research with the development of mechanical explanations of gravitation. In 1856 August Krönig (probably after reading a paper of Waterston) created a simple gas-kinetic model, which only considered the translational motion of the particles. [8]
In 1857 Rudolf Clausius, according to his own words independently of Krönig, developed a similar, but much more sophisticated version of the theory which included translational and contrary to Krönig also rotational and vibrational molecular motions. In this same work he introduced the concept of mean free path of a particle. [9] In 1859, after reading a paper by Clausius, James Clerk Maxwell formulated the Maxwell distribution of molecular velocities, which gave the proportion of molecules having a certain velocity in a specific range. This was the first-ever statistical law in physics.[10] In his 1873 thirteen page article 'Molecules', Maxwell states: “we are told that an 'atom' is a material point, invested and surrounded by 'potential forces' and that when 'flying molecules' strike against a solid body in constant succession it causes what is called pressure of air and other gases.”[11] In 1871, Ludwig Boltzmann generalized Maxwell's achievement and formulated the Maxwell–Boltzmann distribution. Also the logarithmic connection between entropy and probability was first stated by him.
In the beginning of twentieth century, however, atoms were considered by many physicists to be purely hypothetical constructs, rather than real objects. An important turning point was Albert Einstein's (1905)[12] and Marian Smoluchowski's (1906)[13] papers on Brownian motion, which succeeded in making certain accurate quantitative predictions based on the kinetic theory.
disebabkan oleh denyut-denyut statis di antara molekul-molekul, seperti yang diduga Isaac Newton, melainkan disebabkan oleh tumbukan antarmolekul yang bergerak pada kecepatan yang berbeda-beda. Teori Kinetik dikenal pula sebagai Teori Kinetik-Molekular atau Teori Tumbukan atau Teori Kinetik pada Gas.
Postulat
Teori untuk gas ideal memiliki asumsi-asumsi berikut ini:- Gas terdiri dari partikel-partikel sangat kecil, dengan [[massa] tidak nol.
- Banyaknya molekul sangatlah banyak, sehingga perlakuan statistika dapat diterapkan.
- Molekul-molekul ini bergerak secara konstan sekaligus acak. Partikel-partike yang bergerak sangat cepat itu secara konstan bertumbukan dengan dinding-dinding wadah.
- Tumbukan-tumbukan partikel gas terhadap dinding wadah bersifat lenting (elastis) sempurna.
- Interaksi antarmolekul dapat diabaikan (negligible). Mereka tidak mengeluarkan gaya satu sama lain, kecuali saat tumbukan terjadi.
- Keseluruhan volume molekul-molekul gas individual dapat diabaikan bila dibandingkan dengan volume wadah. Ini setara dengan menyatakan bahwa jarak rata-rata antarpartikel gas cukuplah besar bila dibandingkan dengan ukuran mereka.
- Molekul-molekul berbentuk bulat (bola) sempurna, dan bersifat lentur (elastic).
- Energi kinetik rata-rata partikel-partikel gas hanya bergantung kepada suhu sistem.
- Efek-efek relativistik dapat diabaikan.
- Efek-efek Mekanika kuantum dapat diabaikan. Artinya bahwa jarak antarpartikel lebih besar daripada panjang gelombang panas de Broglie dan molekul-molekul dapat diperlakukan sebagai objek klasik.
- Waktu selama terjadinya tumbukan molekul dengan dinding wadah dapat diabaikan karena berbanding lurus terhadap waktu selang antartumbukan.
- Persamaan-persamaan gerak molekul berbanding terbalik terhadap waktu.
Teori Kinetik juga telah diperluas untuk memasukkan tumbukan tidak lenting di dalam materi butiran oleh Jenkins dan kawan-kawan.[rujukan?]
[sunting] Faktor
[sunting] Tekanan
Tekanan dijelaskan oleh teori kinetik sebagai kemunculan dari gaya yang dihasilkan oleh molekul-molekul gas yang menabrak dinding wadah. Misalkan suatu gas denagn N molekul, masing-masing bermassa m, terisolasi di dalam wadah yang mirip kubus bervolume V. Ketika sebuah molekul gas menumbuk dinding wadah yang tegak lurus terhadap sumbu koordinat x dan memantul dengan arah berlawanan pada laju yang sama (suatu tumbukan lenting), maka momentum yang dilepaskan oleh partikel dan diraih oleh dinding adalah:Partikel memberi tumbukan kepada dinding sekali setiap 2l/vx satuan waktu (di mana l adalah panjang wadah). Kendati partikel menumbuk sebuah dinding sekali setiap 1l/vx satuan waktu, hanya perubahan momentum pada dinding yang dianggap, sehingga partikel menghasilkan perubahan momentum pada dinding tertentu sekali setiap 2l/vx satuan waktu.
Besaran kecepatan untuk tiap-tiap partikel mengikuti persamaan ini:
Misalkan ada sejumlah besar partikel yang bergerak cukup acak, gaay pada tiap-tiap dinding akan hampir sama dan kini perhatikanlah gaya pada satu dinding saja, kita punya:
 dapat dituliskan sebagai
dapat dituliskan sebagai 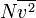 , di mana garis atas menunjukkan rata-rata, pada kasus ini rata-rata semua partikel. Kuantitas ini juga dinyatakan dengan
, di mana garis atas menunjukkan rata-rata, pada kasus ini rata-rata semua partikel. Kuantitas ini juga dinyatakan dengan  di mana vrms dalah akar kuadrat rata-rata kecepatan semua partikel.
di mana vrms dalah akar kuadrat rata-rata kecepatan semua partikel.Jadi, gaya dapat dituliskan sebagai:
Jadi, karena luas bagian yang berseberangan dikali dengan panjang sama dengan volume, kita punya pernyataan berikut untuk tekanan
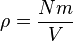 .
.Maka tekanan adalah
 yakni suatu sifat mikroskopik. Ketahuilah bahwa hasil kali tekanan dan volume adalah sepertiga dari keseluruhan energi kinetik.
yakni suatu sifat mikroskopik. Ketahuilah bahwa hasil kali tekanan dan volume adalah sepertiga dari keseluruhan energi kinetik.[sunting] Suhu dan energi kinetik
Dari hukum gas ideal-
- PV = NkBT(1)
Derivat:
-

 (2)
(2)

Suhunya menjadi
-
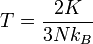 (3)
(3)
| “ | Rerata energi kinetik molekuler adalah sebanding dengan suhu absolut. | ” |
-
 (4)
(4)
Karena 3N adalah derajat kebebasan (DK) dalam sebuah sistem gas monoatomik dengan N partikel, energi kinetik tiap DK adalah:
-
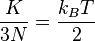 (5)
(5)
- Tiap mole: 12.47 J
- Tiap molekul: 20.7 yJ = 129 μeV
- Tiap mole: 3406 J
- Tiap molekul: 5.65 zJ = 35.2 meV
[sunting] Banyaknya tumbukan dengan dinding
Jumlah tumbukan atom dengan dinding wadah tiap satuan luar tiap satuan waktu dapat diketahui. Asumsikan pada gas ideal, derivasi dari [2] menghasilkan persamaan untuk jumlah seluruh tumbukan tiap satuan waktu tiap satuan luas:[sunting] Laju RMS molekul
Dari persamaan energi kinetik dapat ditunjukkan bahwa:[sunting] Banyaknya tumbukan dengan dinding
One can calculate the number of atomic or molecular collisions with a wall of a container per unit area per unit time.Assuming an ideal gas, a derivation[3] results in an equation for total number of collisions per unit time per area:
[sunting] Laju RMS molekul
From the kinetic energy formula it can be shown that[sunting] Sejarah
In 1738 Daniel Bernoulli published Hydrodynamica, which laid the basis for the kinetic theory of gases. In this work, Bernoulli positioned the argument, still used to this day, that gases consist of great numbers of molecules moving in all directions, that their impact on a surface causes the gas pressure that we feel, and that what we experience as heat is simply the kinetic energy of their motion. The theory was not immediately accepted, in part because conservation of energy had not yet been established, and it was not obvious to physicists how the collisions between molecules could be perfectly elastic.Other pioneers of the kinetic theory (which were neglected by their contemporaries) were Mikhail Lomonosov (1747),[4] Georges-Louis Le Sage (ca. 1780, published 1818),[5] John Herapath (1816)[6] and John James Waterston (1843),[7] which connected their research with the development of mechanical explanations of gravitation. In 1856 August Krönig (probably after reading a paper of Waterston) created a simple gas-kinetic model, which only considered the translational motion of the particles. [8]
In 1857 Rudolf Clausius, according to his own words independently of Krönig, developed a similar, but much more sophisticated version of the theory which included translational and contrary to Krönig also rotational and vibrational molecular motions. In this same work he introduced the concept of mean free path of a particle. [9] In 1859, after reading a paper by Clausius, James Clerk Maxwell formulated the Maxwell distribution of molecular velocities, which gave the proportion of molecules having a certain velocity in a specific range. This was the first-ever statistical law in physics.[10] In his 1873 thirteen page article 'Molecules', Maxwell states: “we are told that an 'atom' is a material point, invested and surrounded by 'potential forces' and that when 'flying molecules' strike against a solid body in constant succession it causes what is called pressure of air and other gases.”[11] In 1871, Ludwig Boltzmann generalized Maxwell's achievement and formulated the Maxwell–Boltzmann distribution. Also the logarithmic connection between entropy and probability was first stated by him.
In the beginning of twentieth century, however, atoms were considered by many physicists to be purely hypothetical constructs, rather than real objects. An important turning point was Albert Einstein's (1905)[12] and Marian Smoluchowski's (1906)[13] papers on Brownian motion, which succeeded in making certain accurate quantitative predictions based on the kinetic theory.
| Robert Boyle : Hukum Boyle |  |  |  |
 Robert Boyle
(25 Januari 1627 - 30 Desember 1691) adalah ahli fisika Inggris,
pengarang, Bapak Ilmu Kimia, penemu hukum Boyle, penemu pompa hampa
udara, penemu konsep atom, orang pertama di dunia yang membedakan unsur
dari senyawa, asam dari alkali, orang pertama di dunia yang menemukan
pentingnya udara bagi pernafasan, pembakaran, dan kehidupan, orang
pertama di dunia yang menemukan bahwa suara tak dapat merambat di dalam
tabung hampa. Boyle menekankan pentingnya eksperimen yang cermat bagi
perkembangan ilmu. Ia membuat eksperimen dengan luas tentang proses
pemanasan logam. Ia mnemukan gejala penguapan dan pembekuan.
Robert Boyle
(25 Januari 1627 - 30 Desember 1691) adalah ahli fisika Inggris,
pengarang, Bapak Ilmu Kimia, penemu hukum Boyle, penemu pompa hampa
udara, penemu konsep atom, orang pertama di dunia yang membedakan unsur
dari senyawa, asam dari alkali, orang pertama di dunia yang menemukan
pentingnya udara bagi pernafasan, pembakaran, dan kehidupan, orang
pertama di dunia yang menemukan bahwa suara tak dapat merambat di dalam
tabung hampa. Boyle menekankan pentingnya eksperimen yang cermat bagi
perkembangan ilmu. Ia membuat eksperimen dengan luas tentang proses
pemanasan logam. Ia mnemukan gejala penguapan dan pembekuan.Masa Belajar. Boyle lahir di Puri Limore di Propinsi Munster, Irlandia, pada tanggal 25 Januari 1627. Karena lahir di Irlandia, ia sering di sebut ahli fisika dan kimia Irlandia. Ia tidak tamat SD dan tidak pernh kawin. Ia meninggal di London pada tanggal 30 Desember 1691 pada umur 64 tahun. Ia berasal dari keluarga besar dan berpengaruh. Anak ayahnya ada 15 orang dan ia anak yang ke 7. Ayahnya mendapat gelar bangsawan, ialah Earl of Cork. Boyle anak yang sangat cerdas dan sangat rajin sekali belajar. Segera setelah ia dapat membaca ia lalu belajar bahasa Latin dan Prancis.
Pada
umur 8 tahun ia bersekolah di SD Eton, sebuah sekolah yang terkenal
dan sebagian muridnya terdiri dari anak-anak orang kaya.Tapi rupanya
boyle terlalu pandai bila bersekolah dengan anak-anak seusianya. Ia
bosan di sekolah tersebut. Maka ia terpaksa keluar dan belajar sendiri
di rumah dengan bimbingan seorang guru. Kemudian ia mengadakan
perjalanan keliling Eropa, antara lain ke Prancis, Swiss, dan Itali. Di
Prancis ia membaca karya-karya Descarter. Di Itali ia membaca
karya-karya Galileo. Waktu itu Galileo masih hidup meskipun sudah tua.
Galileo mninggal pada tahun 1642 ketika boyle berumur 15 tahun. Tapi tulisan-tulisa Galileo tentang bingtang membakar semangat Boyle hingga seluruh hidupnya ia curahkan untuk perkembangan ilmu dan agama. Ketika di Geneva, Swiss ia sangat terkesan oleh kilat dan halilintar yang sangat hebat, hingga sejak itu ia kagum akan besarnya kekuasaan
 Tuhan.
Tuhan.
Eksperimen.
Di Inggris ia tinggal bersama Katherine, kakak perempuanya yang
sekarang sudah menjadi nyonya Ranelagh. Katherine memperkenalkan Boyle
kepada orang-orang penting, antara lain kepada Samuel Hartlih, pembaru
pendidikan dan pertanian Hartlib meyakinkan boyle bahwa system
pendidikan pada waktu itu salah, lebih-lebih di universitas-universitas
di Inggris masih membebek ajaran aristoteles yang tidak selalu benar.
Hartlib mendorong Boyle supaya mencari kebenaran ilmiah lewat
eksperimen, bukan hanya dengan teori saja. Untunglah Boyle tidak pernah
duduk di universitas. Dengan demikian,ia terselamatkan dari system
pendidikan yang kurang menguntungkan.
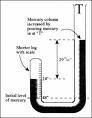
Pompa Hampa Udara. Karena gangguan perang saudara, pada tahun 1654 Boyle p indah ke Oxford. Disini ia mendirikan laboratorium sederhana Ia mulai mengadakan eksperimen dengan sungguh-sungguh. Pada tahun 1657 Boyle mendengar penemuan dan eksperimen Guericke, ahli fisika Jerman. Guericke menemukan pompa hampa udara pada tahun 1650. Guericke menemukan bahwa cahaya dapat menerobos tabung hampa udara tapi bunyi tidak. Boyle segera meminta bantuan Robert Hooke untuk membuat pompa hampa udara.Boyle dan Hooke adalah orang yang menemukan pompa hampa udara yang pertama di Inggris. Boyle mengadakan eksperimen seperti Guericke. Ia juga menemukan bahwa bunyi tidak dapat menerobos tabung udara Tapi eksperimen Boyle tidak berhenti hanya sampai disini.
Pompa Hampa Udara. Karena gangguan perang saudara, pada tahun 1654 Boyle p indah ke Oxford. Disini ia mendirikan laboratorium sederhana Ia mulai mengadakan eksperimen dengan sungguh-sungguh. Pada tahun 1657 Boyle mendengar penemuan dan eksperimen Guericke, ahli fisika Jerman. Guericke menemukan pompa hampa udara pada tahun 1650. Guericke menemukan bahwa cahaya dapat menerobos tabung hampa udara tapi bunyi tidak. Boyle segera meminta bantuan Robert Hooke untuk membuat pompa hampa udara.Boyle dan Hooke adalah orang yang menemukan pompa hampa udara yang pertama di Inggris. Boyle mengadakan eksperimen seperti Guericke. Ia juga menemukan bahwa bunyi tidak dapat menerobos tabung udara Tapi eksperimen Boyle tidak berhenti hanya sampai disini.
Hukum Boyle 1622. Boyle menemukan bahwa udara dapat dimanfaatkan dan dapat berkembang bila dipanaskan. Akhirya ia mnemukan hukum yang kemudian terkenal sebagai hukum Boyle:” bila suhu tetap, volume gas dalam ruangan tertutup berbanding terbalik dengan tekananya”
Ahli kimia pertama. Dalam sejarah ilmu kimia terdapat beberapa tahap, antara lain tahap alkemi, tahap ilmu kimia. dan tahap ilmu kimia modern Boyle adalah bapak ilmu kimia, sedangkan Lavoisier adalah bapak ilmu kimia modern. Mengapa Boyle disebut bapak ilmu kimia? karena ia mengadakan eksperimen secara ilmiah. Karena ia menemukan konsep atom. Karena ia dapat membedakan unsur senyawa dan campuran. Ia dapat membedakan asam, basa dan alkali. Para ahli sebelumnya tidak dapat. Misalnya Aristoteles, ahli filsafat Yunani yang terbesar, mengira air, tanah, api, dan udara, adalah unsur.
Ahli kimia pertama. Dalam sejarah ilmu kimia terdapat beberapa tahap, antara lain tahap alkemi, tahap ilmu kimia. dan tahap ilmu kimia modern Boyle adalah bapak ilmu kimia, sedangkan Lavoisier adalah bapak ilmu kimia modern. Mengapa Boyle disebut bapak ilmu kimia? karena ia mengadakan eksperimen secara ilmiah. Karena ia menemukan konsep atom. Karena ia dapat membedakan unsur senyawa dan campuran. Ia dapat membedakan asam, basa dan alkali. Para ahli sebelumnya tidak dapat. Misalnya Aristoteles, ahli filsafat Yunani yang terbesar, mengira air, tanah, api, dan udara, adalah unsur.
 Konsep Atom.
Kira-kira pada tahun 400 SM, Demokritos, ahli filsafat Yunani,
mengutarakan bahwa semua benda terdiri dari atom. Tapi selama hampir
2000 tahun pendapat itu dilupakan orang, karena para ahli lebih suka
mengikuti ajaran Aristoteles yang teryata keliru Menurut Aristoteles
semua benda terdiri dari air, tanah, udara, dan api. Paracelcus, ahli
fisika Swiss berpendapat bahwa semua benda terdiri dari merkuri,
belerang dan garam. Van Helmont, ahli kimia Belgia mengira bahwa semua
benda terdiri dari udara dan air.
Konsep Atom.
Kira-kira pada tahun 400 SM, Demokritos, ahli filsafat Yunani,
mengutarakan bahwa semua benda terdiri dari atom. Tapi selama hampir
2000 tahun pendapat itu dilupakan orang, karena para ahli lebih suka
mengikuti ajaran Aristoteles yang teryata keliru Menurut Aristoteles
semua benda terdiri dari air, tanah, udara, dan api. Paracelcus, ahli
fisika Swiss berpendapat bahwa semua benda terdiri dari merkuri,
belerang dan garam. Van Helmont, ahli kimia Belgia mengira bahwa semua
benda terdiri dari udara dan air.Pada tahun 1661 Boyle menghidupkan kembali ajaran Demokritos. Ia mengungkapkan dalam bukunya yang berjudul The Sceptical Chymist (Ahli Kimia Yang Sangsi). Dalam bukunya itu Boyle menyerang ajaran Aristoteles dan Paracelsus. Ia mencela Aristoteles yang memandang benda dari segi forma dan kualitas. Boyle menyatakan bahwa semua benda terdiri dari atom, Adanya zat yang beraneka ragam disebabkan karena jumlah atom, kedudukan atom, gerak atom, dan susunan atom. Karena jasa Boyle, ilmu fisika dan kimia diluruskan ke jalur yang benar.
Langganan:
Postingan (Atom)
Blogger news
About Me
- Kyki's Blog
Diberdayakan oleh Blogger.
Blogroll
Welcome To Kyki's Blog. I build this blog in order to share information or knowledge that I know. Hopefully this blog useful. Thanks
Popular Posts
-
Reaksi kimia merupakan contoh yang paling sesuai untuk perubahan kimia. Pada reaksi kimia, satu zat atau lebih diubah menjadi zat baru. Zat...
-
DEPARTEMEN PENDIDIKAN NASIONAL DIRJEN MANAJEMEN PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PENDIDIKAN MENENGAH UMUM TEST SELEKSI TINGKAT PROVI...
-
ACTIVE AND PASSIVE VOICE Kalimat Aktif dan Kalimat Pasif Kata kerja transitif mempunyai dua voice (ragam gramatikal), aktif dan pas...
-
SOAL-SOAL DEKLARASI 1. Manakah yang mendeklarasikan tipe enumerasi dengan tepat? a. Type a=integer; b. Type a=1..300; c. Type a=(baik, jelek...
-
Procedure, Narrative And Expressions Procedure How to make Lemonade Ingredients: For each glass use: - 2 tablespoons of lemon jui...
-
SUKU BANYAK Suku banyak (polinomial) adalah sebuah ungkapan aljabar yang variabel (peubahnya) berpangkat Bilangan bulat non negative. B...
-
integral di 07:15 Integral adalah kebalikan dari proses diferensiasi. Integral ditemukan menyusul ditemukannya masalah dalam diferensiasi ...
-
Teknik Lempar Cakram Yang Baik. Lempar cakram adalah salah satu cabang olahraga athletik. Lempar cakram diperlombakan sejak Olimpi...
-
DEFINITION : Advertising is a form of communication intended to persuade an audience (viewers, readers or listeners) to purchase or take s...
-
Tidak jarang para pelajar sekolah ataupun peserta kursus Bahasa Inggris mendapatkan tugas untuk membuat conto...
Follow This Blog
Blogger templates
Tags
- Bahasa Arab Kelas XII (2)
- Bahasa Indonesia SMA X (3)
- Bahasa Indonesia SMA XI (3)
- Bahasa Indonesia SMA XII (3)
- Bahasa Inggris SMA X (3)
- Bahasa Inggris SMA XI (3)
- Bahasa Inggris SMA XII (3)
- Bahasa Jepang Kelas XII (3)
- Biologi Kelas XII (2)
- Biologi SMA X (3)
- Biologi SMA XI (3)
- Biologi SMA XII (3)
- Ekonomi SMA X (3)
- Fisika SMA X (3)
- Fisika SMA XI (3)
- Fisika SMA XII (3)
- Geografi SMA X (3)
- Kimia SMA X (3)
- Kimia SMA XI (3)
- Kimia SMA XII (3)
- Kitty Wedding (1)
- Matematika SMA X (3)
- Matematika SMA XI (3)
- Matematika SMA XII (3)
- OSN Astronomi (1)
- OSN Biologi (1)
- OSN Ekonomi (1)
- OSN Fisika (1)
- OSN Kebumian (1)
- OSN Kimia (1)
- OSN Matemika (1)
- OSN Tik (1)
- Pend. Agama Islam SMA X (3)
- Pend. Agama Islam SMA XI (3)
- Pend. Agama Islam SMA XII (3)
- Penjaskes SMA X (3)
- Penjaskes SMA XI (3)
- Penjaskes SMA XII (3)
- Pkn SMA X (3)
- Pkn SMA XI (3)
- Pkn SMA XII (3)
- Sejarah SMA X (3)
- Sejarah SMA XI (3)
- Sejarah SMA XII (3)
- Seni budaya kelas XII (2)
- Sosiologi SMA X (3)
- Terselubung (3)
- TIK SMA XI (2)
- TIK SMA XII (2)
- TIK SMA XIII (1)
Blog archive
-
▼
2012
(125)
-
▼
Mei
(51)
- KilesKitty:)
- Program Linear
- BARISAN DAN DERET
- Aplikasi Gerak Harmonik Sederhana
- metebolisme dan katabolisme
- genetika
- ACCUSING, DENYING, APOLOGIZING
- Functional Skills
- Sejarah umum seni lukis
- MOZAIK
- ANCAMAN DISINTEGRASI BANGSA
- KONFLIK INDONESIA-BELANDA TAHUN 1945-1949
- PERKEMBANGAN POLITIK DAN EKONOMI SERTA PERUBAHAN M...
- Macromedia Kelas XII
- Pengenalan Grafis Berbasis Vektor dan Berbasis Bitmap
- Power Point
- pancasila Sebagai Dasar Negara (PKN XII)
- Sistem Pemerintahan
- Peranan pers dalam masyarakat demokrasi,
- senam lantai
- lempar lembing
- KARATE
- integral
- UNSUR-UNSUR GOLONGAN UTAMA
- SIFAT KOLIGATIF
- SEL ELEKTROLISIS
- Persamaan Gerak Harmonik Sederhana
- gerak harmonik
- genetika
- REPRODUKSI SEL
- metebolisme dan katabolisme
- DAI IK KA
- DAI SAN KA
- DAI GO KA
- A LETTER
- PIDATO
- LAPORAN HASIL SEMINAR
- surat lamaran
- KEHIDUPAN SEHARI-HARI
- Beberapa Contoh Ucapan Selamat dan Tegur Sapa dala...
- MUNAKAHAT
- IMAN KEPADA QADA DAN QADAR ALLAH SWT
- Pengertian Hari Kiamat
- Tik
- Matematika
- Kimia
- Kebumian
- Fisika
- Ekonomi
- Biologi
- Astronomi
-
▼
Mei
(51)